It is increasingly the practice of financial institutions to assess the exposure of their commercial loan portfolios to credit loss on the basis of models of portfolio value at risk (VAR). Four different approaches to the calculation of credit portfolio VAR are documented in references [1] through [4]. (See reference [5] for a taxonomy and comparison of these approaches.) One application of such credit VAR models is in developing risk capital "rules," i.e., quantitative guidelines for allocating risk capital to individual loan transactions. At issue is whether the application of such risk capital rules actually results in an adequate allocation of portfolio risk capital.

In the case of exposure to market risk, the standard capital allocation criterion is that the lender must hold sufficient capital to cover unexpected portfolio loss at a specified risk horizon and to a specified confidence level (see reference [6]). One possibility would be to adapt the same criterion to credit exposures. That in fact is the approach taken in the credit VAR models in references [1] through [4]. We propose instead to gauge the adequacy of the amount of capital allocated to a credit portfolio by testing whether that capital is sufficient to earn the portfolio a target credit rating.

For this we need to define what constitutes a credit portfolio default. The "solvency" criterion we apply is that at any given time a lender must hold sufficient capital to survive the hypothetical liquidation of his current loan portfolio. As a credit inter-mediary, the lender must meet his obligations as a borrower from a combination of the profits (if any) he realizes from his portfolio revenues prior to the portfolio sale, the proceeds from the portfolio sale, and the risk capital he has dedicated to the portfolio at the time of the sale. If the capital adequacy test fails, then a portfolio default is considered to occur at the point in time that the portfolio is sold and it is determined that the lender lacks the capital to settle with his creditors.

We observe that the application of the capital adequacy test requires a loan transaction pricing model that can (i) value the cash flows of individual loans held in the lender’s portfolio, and (ii) estimate the fair market value of the loans that are sold. The Loan Analysis System^SM (LAS) is such a loan transaction pricing model (see reference [7]).

We proceed to describe the specifics of the portfolio capital adequacy test and the computational methods used in its application. Some of the mathematical details appear in the appendix.

Risk Capital Adequacy Criterion

The starting point of portfolio risk capital analysis is the basic notion of "unexpected loss," i.e., the amount by which actual portfolio return falls short of expected portfolio return. Note that the reference against which portfolio loss is measured for purposes of capital allocation is expected return rather than zero return.

With this interpretation of portfolio loss, the issue becomes how to measure portfolio return. We take the following point of view. At time t, the lender makes the necessary disbursements of principal to "originate" his actual loan portfolio . The assumed ground rules for the portfolio liquidation process are that the lender is obliged to service the portfolio  until such time as he can sell those loans still on his books, but he can write no new loans. When the lender finds a buyer (at time ), the remaining loans in  are sold at their then current mark-to-market values. In determining the mark-to-market value of the lender’s portfolio, we use risk-neutral pricing as derived from observed market par credit spreads. The lending operation is considered to remain "solvent" throughout this portfolio liquidation process if at its completion the lender’s allocated risk capital is sufficient to cover any unexpected portfolio loss.

The presumption is that the time of sale of the lender’s portfolio can not be predicted with certainty when the liquidation process begins, although a time limit may be imposed. The risk horizon T thus becomes a random variable. The cash flows that take place over the risk interval are those of the lender’s actual portfolio. We denote by  the net position (in time  dollars) of the lender after the loan portfolio has been liquidated and the lenders creditors have (to the extent possible) been repaid.

It is the quantity  that we take to be the lender’s portfolio return over . If  is less than the expected portfolio return , then the lender is considered to have experienced an unexpected loss in the amount

            (1)

We observe that credit default losses are only one of the potential sources of portfolio value loss contributing to . If a loan is not grid priced, then its mark-to-market value will decrease in response to any downward migration in the rating of the borrower. Even if a loan is grid priced, the pricing grid may be poorly calibrated to market credit spreads. It that case loan values may still be adversely affected by downward credit migrations. A general increase in par credit spreads caused by a worsening of economic conditions and a corresponding increase in default rates will cause the lender’s portfolio to lose value across the board. The penalty-free prepayment of a term loan that is "in the money" to the lender creates a loss in portfolio value, as does the likely increase in utilization of a revolver by a borrower whose credit quality has declined.

To properly assess portfolio exposure, one must account for all of the factors that can affect loan values and potentially contribute to portfolio losses. A detailed accounting of individual loan values is an essential feature of LAS and of the portfolio approach we are proposing.

Let  denote the amount of risk capital the lender allocates to his loan portfolio at time  if he follows the dictates of his risk capital rules. The capital  is considered to be bound to the portfolio at time  and must be held in a risk-free account earning the risk-free return.

Let  denote the amount of capital at time t that the lender has available to allocate to his loan portfolio. Some portion of  might be "time-shared," in the sense that it is committed to liquid investments that carry some degree of risk. Some fraction of the value of these investments is viewed as the equivalent of cash and potentially available for reallocation by the lender to his loan portfolio in order to remain in compliance with his risk capital rules.

The distinction between  and  is an essential one. The quantity  is derived from the lender’s VAR model and is the amount of capital the lender’s risk capital rules direct him to fully commit to his loan portfolio. The presumption is that the lender will follow the guidance of his risk capital rules. Therefore, the lender’s risk-adjusted return on capital (RAROC) at time t is appropriately measured relative to . By contrast,  is determined by the lender’s actual capital resources. It is the size of the pool of capital that the lender can draw from to allocate risk capital to his loan portfolio in accordance with his risk capital rules. In that regard,  is the standard against which compliance with regulatory capital requirements is appropriately judged.

There are then two tests that must be met for the lender’s portfolio to be adequately capitalized: (i)  and (ii) . The first of these two conditions enforces the requirement that the lender must allocate sufficient risk capital to his loan portfolio under his risk capital rules to offset his unexpected portfolio loss. The condition  is therefore really a test of the lender’s risk capital rules. The condition enforces the requirement that the lender have access to sufficient risk capital to comply with his risk capital rules. Neither of these conditions can be met with absolute certainty. A probabilistic treatment is therefore required.

Combining the two conditions, the lender will have adequate risk capital provided:

.            (2)

Suppose we identify a violation of the above requirement with a "portfolio default." Then, conditioned on , the probability  of a portfolio default is given by

.             (3)

If the lender originates and then immediately sells the loan portfolio, i.e., if , then his portfolio return (whether positive or negative) becomes predictable. The lender’s unexpected loss is then zero (i.e., ) and there is no requirement for him to hold risk capital. It follows that  and . For , it is always the case that .

We assume that the lender has set a target credit rating grade g for his commercial lending line of business. The rating grade g implies a cumulative probability of default curve  based on published default statistics for a g-rated company. Let  denote the maximum maturity of any loan in  (i.e., the effective portfolio maturity) and let  be the probability density for the time T to liquidate . Suppose one imposes the requirement that  for. Then for 

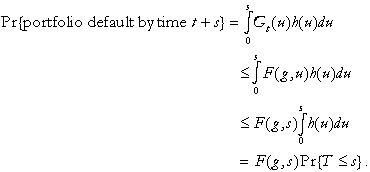(4)

It thus follows that independently of the density ,

        (5)

In fact, from (4) one obtains the stronger condition

           (6)

Suppose that the hard deadline  is imposed on the portfolio liquidation process. Then it follows from (6) that then the cumulative probability of portfolio default prior to time  given compliance with the deadline is bounded above by .

We are thus led to the following risk capital adequacy test relative to risk rating g:

The portfolio  at time t is assigned the credit rating grade g provided that  for  , but the analogous test fails for any higher grade.

This test takes into explicit account the individual transactions that comprise , the capital allocation rules that the lender applies at the transaction level, and the amount of risk capital held by the lender at time t that is available to support .

Suppose that the regulatory requirement for a commercial loan portfolio was that the portfolio must earn a minimum portfolio credit rating . Then the regulatory capital requirement for the portfolio  would be the minimum value of  such that the condition  is met for .

To provide some insight into the application of the capital adequacy test, consider a situation in which credit conditions deteriorate to the point that the test fails. Some remedial action would then be required on the part of the lender. One possibility is for the lender to eliminate some of the more risky loans in an effort to reduce his credit loss exposure. Another possibility is for the lender to allocate additional risk capital to his loan portfolio through some combination of freeing up capital committed to other enterprises (thereby increasing ) and increasing risk capital allocations at the transaction level. The latter could be achieved through some combination of increasing par credit spreads and accepting a lower risk capital hurdle rate.

Since so many factors affect portfolio exposure, there is no simple algorithmic procedure for transforming an undercapitalized loan portfolio into one that is adequately capitalized. Nonetheless, the methods we have described can be used to identify that a portfolio is undercapitalized, to test alternative portfolio restructuring strategies, and to confirm that as the result of a set of actions, the lender’s portfolio now earns the targeted risk rating.

In the section that follows and in the appendix, we describe the computational methods used to construct the critical portfolio default distribution  used in testing risk capital adequacy.

Computational Procedure

The calculation of the cumulative portfolio default probability  proceeds in two stages. The first stage is at the individual transaction level and makes use of backward time recursive methods in the context of a discrete time and discrete state valuation grid. The second stage uses forward time recursive methods and Monte Carlo simulation methods in combination.

Transaction Level. The discrete times  used in the valuation grid can be chosen somewhat arbitrarily, but should include all of the times at which the cash flows associated with a given transaction can occur. As we proceed to describe, the state associated with a transaction at any specified time is represented by a 3-vector .

The variate  models an assumed systematic or "business cycle" effect that influences both interest rates and the credit rating migration of each borrower. We refer the reader to references [9] and [10] for a description of the stochastic process model for , a discussion of the empirical evidence supporting the existence of , and an outline of the statistical procedure used to estimate  from historical rating grade migration data.

In the case of interest rates,  is taken to be one of the two factors in a Heath-Jarrow-Morton (HJM) two-factor term structure model for forward interest rates, specialized such that each factor is scaled by an exponentially decaying volatility function (see reference [11]). The variate  is the second factor of this HJM model. We model  and  as statistically correlated. Each HJM model factor depends on two model parameters, a spot volatility and a decay rate that determines how quickly the factor volatility falls off with increasing maturity. These parameters and the initial forward rate curve are calibrated to a combination of observed interest rates and interest rate securities prices.

The third state variable is the borrower risk grade . Migration in rating grade is based on the continuous risk rating model as initially described in reference [1] and subsequently modified in reference [8] for the effect of systematic credit risk. The migration process is modeled as Markovian in the state  rather than in the state  alone. Every entry in the migration matrix is a function of . Positive values of  induce an upward (improved rating) bias in rating migration, negative values a downward bias.

In addition to modulating the migration probabilities, the variate  affects the probability distribution for loss in the event of default (LIED) and affects the forward structure of par credit spreads. The LIED effect of  is on the mean and standard deviation of the LIED distribution. Through its effect both on rating migration probabilities and the LIED distribution,  impacts the volatility of loan returns. A functional relationship between the risk premium (unexpected loss) component of par credit spreads and the volatility of loan returns is postulated and calibrated to observed credit spreads.

Two important quantities calculated and stored at each node of the valuation grid are: (i) the mark-to-market value of the transaction at the given node and (ii) the risk capital allocated to the transaction at the given node. These quantities are used in the portfolio level calculations to obtain . The valuation grid is filled in using a recursive algorithm that proceeds backward in time from the time  that the transaction matures to the time  that the transaction is originated. The basic approach is an extension of the procedure first described in [13] and subsequently incorporated into the Loan Analysis System^SM developed by KPMG Peat Marwick.

Portfolio Level. Mark-to-market value, cumulative net cash flow, and allocated risk capital are each naturally additive over transactions. If only expected values at the portfolio level were of interest, the lack of statistical independence across transactions would be of no concern and in each case one could simply sum expected values at the transaction level to obtain the corresponding expected value at the portfolio level. However, the calculation of  requires dealing with probability distributions, not just expected values. Therefore, correlation between transactions is an issue.

The approach we take is to decouple the stochastic processes governing the state vectors of the individual transactions by conditioning on the specific path  of the  process through time . Conditioning on  identifies through time  both the path of interest rates under the assumed two-factor HJM model and the evolution of the systematic component of the credit rating migration process. We refer to such a path as an economic scenario. What is important is that conditioned on such an economic scenario, the state processes of the individual transactions are governed entirely by borrower specific credit risk and are therefore mutually independent.

Let  denote the 3-vector with components:
 
 

Then it is a consequence of the central limit theorem that the conditional distribution of  given  can be closely approximated as multivariate Gaussian. The mean vector and covariance matrix of this 3-variate Gaussian distribution can be calculated from the conditional means and conditional covariances of the individual transactions using the conditional independence of the transactions. The required transaction level moments in turn can be calculated from the information stored in the valuation grids for the individual transactions. (See appendix for details.)

An important consequence of the application of the central limit theorem is that the borrower specific state variables disappear. As a result, at the portfolio level there are only two state variables, z and w. All of the relevant information about the individual transactions is encapsulated into the Gaussian variates . The conditional probability of default at  can then be calculated by integrating the (3-variate Gaussian) marginal density for  over the appropriate 3-dimensional region. In particular, this conditional probability calculation can be performed without the need for Monte Carlo simulation.

Thus, the methods described give a procedure for calculating the probability of portfolio default at  conditioned on a specific economic scenario. The user then has two options. The first is to postulate possible scenarios and to "stress test" the portfolio by studying the effect of scenario variation on portfolio default probability. The second is to use Monte Carlo simulation to generate scenarios using the assumed probability model for the  process and to calculate a default probability averaged over scenarios.

We observe that it is only the scenario weights that must be simulated. The conditional default probabilities are obtained using the central limit theorem. This greatly reduces the Monte Carlo sampling error in estimating unconditional default probabilities. This variance reduction is quite important, because in assessing the adequacy of risk capital, one must be able to accurately calculate extreme tail probabilities of the portfolio loss distribution.

The focus of our discussion has been on the calculation of the probability of portfolio default. However, the probability distributions of the components ,  and  of the  vector are also of interest. From the marginal densities of , one can calculate for any future time : (i) the probability distribution for the cumulative portfolio cash flows through , (ii) the probability distribution for the allocated portfolio risk capital at , and (iii) the probability distribution for the mark-to-market value of the lender’s remaining portfolio at . From the density for , one can also determine the probability distribution on portfolio return (as we have defined it).

As noted, the conditional distribution of each of ,  and  is approximately Gaussian for each fixed economic scenario . However, a weighted sum of Gaussian densities can be highly non-Gaussian. We expect, for example, the probability density for portfolio return to exhibit the skewness and extended lower tail that are characteristic of credit portfolio exposures (see, for example, reference [10]).

Both the transaction calculations and the portfolio calculations offer the opportunity to exploit the inherent computational parallelism of the problem. At the transaction level, a queue can be formed with each transaction assigned to the next available processor. Similarly, in calculating the conditional moments of the  distribution from the corresponding transaction level moments, a queue can be formed such that each transaction is assigned to the next available processor. Exploiting such opportunities for parallel computation will require either networking several PC’s or a single system with multiprocessor capability.

The Extension to Portfolios of Loans and Credit Derivatives in Combination

Lenders are increasingly using credit derivatives to hedge selected exposures in their loan portfolios. The methods described above extend in a natural way to portfolios comprised of commercial loans and credit derivatives in combination. The definitions of portfolio return, unexpected portfolio loss, and portfolio default remain unchanged, as does the criterion for the adequacy of portfolio risk capital.

Adding credit derivatives to the lender’s portfolio in general requires dealing with two sources of credit risk, obligor (borrower) credit risk and guarantor (derivative counterparty) credit risk. For example, in the case of a credit default swap, both the credit rating of the obligor and the credit rating of the credit guarantor become state variables. Both of these rating state variables drop out of the problem at the portfolio level. We note that the business cycle variate  is the source of the correlation between the obligor rating migration process and the guarantor rating migration process.

The netting of transactions related to a single borrower is critically important in dealing with loans and credit derivatives in combination. For example, if the lender holds both a loan and a total return swap against the loan, the exposures almost cancel each other. The procedure for netting is a straightforward extension of that for dealing with multiple loans to a single borrower. Before aggregating to the portfolio level, all loans and credit derivatives associated with a given borrower are effectively consolidated into a composite net transaction. For each interest rate scenario, these composite transactions are conditionally independent across borrowers and the application of the central limit theorem as previously described is justified.
 
 

Summary

We have described a test and an associated computational procedure for determining whether a commercial lender’s loan portfolio is adequately capitalized. The test assumes the hypothetical liquidation of the lender’s portfolio and involves two conditions. The first condition is that the allocated risk capital implied by the lender’s risk capital rules must be sufficient to cover unexpected portfolio loss through the completion of the liquidation process. The second condition is that the amount of loan portfolio risk capital available to the lender must be sufficient to enable the lender to comply with his risk capital rules.

There are important differences between the approach we have described and standard VAR methods. The usual approach is to specify a fixed confidence level against which to test risk capital adequacy and to specify a fixed risk horizon at which to apply that test. We replace the fixed confidence level with the target credit rating that the lender has set for his loan portfolio. We replace the fixed risk horizon with the uncertain amount of time required by the lender to liquidate his portfolio.

For capital allocation purposes, portfolio loss is equated not with unexpected credit default loss but with the unexpected shortfall in the lender’s aggregate portfolio return. In calculating portfolio return, account is made for all portfolio cash flows prior to the sale of the portfolio, as well as the proceeds the lender realizes from the portfolio sale at (risk-neutral) market pricing. The test for the adequacy of the risk capital allocated to a loan portfolio is that the portfolio must earn the credit rating targeted by the lender.

The proposed capital adequacy test is directly linked to a loan transaction pricing model. Such a model is required to value the multiperiod cash flows generated by individual loan transactions and to mark loan values to market.
 
 

References

Fix a loan and define

Condition on an economic scenario . This conditioning is implicit in everything that follows.

Define

Then it is necessary to calculate the first and second order moments of the 3-vector  conditioned on . It is from these transaction level moments that one calculates the corresponding portfolio moments of , using the conditional independence of the transactions given .

The quantities  and  are conditionally deterministic for each value of  and are available from the backward recursion stage of the calculation. For each value of , the quantity , because it depends on the entire past history of the borrower’s credit rating, remains a random variable. We develop a recursive procedure for calculating the first and second moments of .

Let

(A-1)

where  is the risk-free discount rate over the interval . Note that  becomes deterministically known once  is specified.

It is easily shown using equation (A-1) that

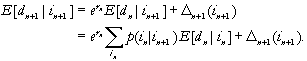(A-2)

Equation (A-2) is the basis for the recursive calculation of the quantities .

The conditional variance recursion is given by:
 

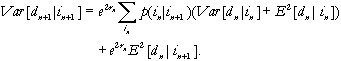(A-3)

Once all of the first and second moments of  conditioned on  have been calculated (the conditioning on  remains implicit), the conditioning on  is removed using the general relations

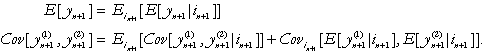(A-4)

Applying the above recursive procedure, one calculates for each n the first and second moments of the Gaussian distribution of  conditioned on . The conditional probability of default at  can then be calculated by integrating the density for  over the appropriate 3-dimensional region. In particular, this calculation can be performed without the need for Monte Carlo simulation.

The distribution of  given  is (closely approximated as) multivariate Gaussian, so each component of  has a marginal univariate Gaussian distribution. The implication is that ,  and  each have a Gaussian distribution. The unconditional distribution of each of these quantities can therefore be approximated as a weighted sum of Gaussian distributions. The interest rate scenarios and their weights can either be input by the user or generated using Monte Carlo simulation.

We have defined  to be the aggregate future value of the net of the loan cash flows at . However, the procedure described above would work equally well for some specific component of the cash flows. For example, one might be interested in just the cumulative value of the loan fees paid by the borrower or in the cumulative default loss experienced by the lender. One can derive counterpart recursive formulas analogous to those given above for  and obtain the first and second moments of the (approximately) Gaussian conditional distribution for the value of the cash flow component of interest given a scenario . One can then construct the corresponding unconditional distribution by using Monte Carlo simulation to generate scenarios.