Monte Carlo Simulation Primer

When we measure a value such as the amount of money left in a portfolio after a fixed number of years, we have an idea that with a certain probability the measured value will fall within a certain range- and that this probability depends on the range of numbers we pick. How could we begin to understand what these probabilities might look like? Suppose we have a portfolio with an initial amount of investment money in it, and we are able to perform the experiment of measuring its final value after some fixed number of years over and over. We could then divide up the range between the lowest final value and the highest final value into segments, and count how many of the final values that were observed fell into each "bin". If we then divide the number of observations in each bin by the total number of observations, we get a picture of how likely it is that our final portfolio value falls within a certain range.

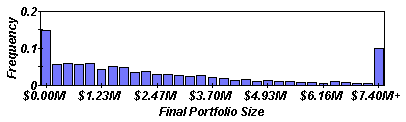
For example in the picture above, we can observe that the final portfolio value falls over 7.4 million dollars about 10% of the time, since about 10% of the observations fall into this bin. And what if we wanted to know about the probability that our measured final value will be less than or equal to a certain key value that we are concerned about? Again we can create a useful picture with our experiment:

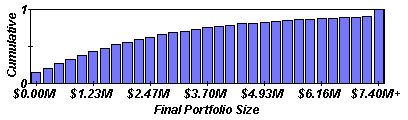
We can "accumulate" the bins in our first picture by adding up all the bins to the left of each partitioning value, so that when we look at our new plot, we can see that the portion of the bin area to the left of each partitioning value (as compared with the total bin area) corresponds to the likelihood that our final value measurement comes out to be less than that partitioning value. For instance, in our plot above we can see that our final portfolio value is less than 1.23 million dollars about 50% of the time.

What is Monte Carlo Simulation?

A value that can be measured and that can take on different values when it is measured, such as portfolio value after a given number of years, is commonly referred to as a random variable. The first type of probability picture we created is called the frequency function, because it shows us the frequency with which our random variable falls in a certain range of numbers. The second type of picture is called the cumulative distribution function because it helps to picture the "accumulated" probability that our random variable falls to the left of a certain value.

Monte Carlo simulation is the idea of using statistical trials to get an approximate solution to a problem. There is a random process (such as the generation of portfolio return) where some parameters of the process are equal to the required quantities of the problem. Since these parameters are not known exactly, many observations are made so that the parameters of the process can be determined approximately.

Experiments using Monte Carlo Simulation

Finding a safe spending level

Suppose we have a portfolio with a certain initial value, and we wish to determine a "safe"after-tax spending level for the portfolio to last some number of years with a certain percentage confidence, let's say 85% confidence. That is, we want to determine how much money we can spend yearly so that we are 85% sure that the portfolio will not run out of money before the specified number of years. For this simplified Applet we assume the portfolio is entirely in a taxed account. Suppose we are able to give these values for our portfolio:

• Return: Average portfolio return; this is the gross return, before taxes and with no correction for inflation.
• Volatility: The typical discrepancy between an annual return and the average annual return. For high yield portfolios this might be 1.5 times the return.
• Inflation: Inflation Percentage
• Tax: Tax Percentage
• Confidence: Percentage confidence we want to have in our answer
• # Years: The number N of years we want the portfolio to last
• Initial Portfolio Value: starting amount in dollars

We can use the idea of Monte Carlo Simulation to model the situation despite uncertainty. We will use a Java applet to help us perform the experiment. There are certain quantities (random variables) depending on the portfolio characteristics above which are observed to closely follow a certain behavior in real life. Our applet creates many observations of each random variable, computes the frequency function in the way we discussed above, and returns a picture of the simulated frequency function and cumulative distribution function for the portfolio value after N years.

Note that the simulations performed by our applets in this primer use a very basic model to get an idea of scenario outcomes. The set of input parameters is extremely simplified when compared with the more realistic portfolio and spending plan characterizations used in Wagner's RSP products.

Try it! Start up the applet by pushing the button below.
(This applet requires your web browser to support Java 1.1 : Netscape 4.06 or Explorer 4.0 and above. Mac OS users must use Explorer--sorry. )

Enter the quantities for your portfolio, or press the "Suggest Values" button to suggest some reasonably realistic values. Then press the "Enter Values" button; a message will appear to let you know if the portfolio characteristics you entered were valid. You can clear your values and start over by pressing "Clear" if desired. When your portfolio characteristics have been accepted, press "Compute Safe Spending" and view the simulated results!

Computing Portfolio Lifetime

Now suppose we want to make a different sort of estimate: we have a portfolio with a certain initial value, and we wish to determine with 85% confidence how many years the portfolio will last if we spend a certain percentage of the portfolio's initial value each year. That is, for our given spending level we want to know the number of years such that 85% of the time we expect that our portfolio will not run out of money before that number of years has passed. Let's say we are able to give these values for our portfolio:

• Return: Average portfolio return; this is the gross return, before taxes and with no correction for inflation.
• Volatility: The typical discrepancy between an annual return and the average annual return. For high yield portfolios this might be 1.5 times the return.
• Inflation: Inflation Percentage
• Tax: Tax Percentage
• Confidence: Percentage confidence we want to have in our answer
• Spending Level: Amount spent yearly, as a percentage of the initial portfolio value
• Initial Portfolio Value: starting amount in dollars

We can use the same Monte Carlo Simulation idea to model the situation despite uncertainty. We will use another Java applet below to perform the second experiment. This time the applet finds the number of years the portfolio is expected to last at the given spending level. The number returned is an integer N; more precisely, if the computation returns a value of N years, this indicates that the portfolio would last between N and N+1 years. The applet then returns a picture of the simulated frequency function and cumulative distribution function for the portfolio value after N years.

Try it! Start up the applet by pushing the button below.
(This applet requires your web browser to support Java 1.1 : Netscape 4.06 or Explorer 4.0 and above. Mac OS users must use Explorer--sorry. )

References

For a more detailed discussion of the mathematics behind the computations performed in the applets, see the following article:
Bernard J. McCabe, Analytic Approximation for the Probability That a Portfolio Survives Forever, Journal of Private Portfolio Management, Vol.1, No. 4, Spring 1999.